Work

AI Research

Deploying Large Language Models on Kinara's Edge AI Processor: Novel Quantization Techniques and Compiler Optimization

• Examined systematic outliers across various Language Model architectures (LLMs) to evaluate their suitability for deployment on edge devices, including llama7b (both base and chat versions), qwen7b, and tiny llama. [1]
• Investigated novel quantization methods for optimizing LLMs including, AWQ, GPTQ, GGUF/GGML. [2][5][6]
• Developed a framework for LLM Smoothing, refining model weights using a modified version of QmniQuant that incorporates smoothing into the input of the down projection layer of the attention block and transitions from dynamic to static quantization. [3][4]
• Implemented Flash attention type tiling and an online normalization calculator for SoftMax to achieve memory-efficient precise attention mechanism on ARA NNPs. [7][8]
• Conducted analysis and pruning of LLM layers using Singular Value Decomposition and Block Importance methods to eliminate less important or redundant layers, thereby enhancing model memory bandwidth. Improved throughput from 2 Tokens/sec to 9 Tokens/sec with minimal decrease in accuracy on lm-eval. [9][10]
• Employed LoRA, QLoRA, and LoRA+ techniques to restore pruned models to achieve SOTA accuracy on lm-eval. [11][12][13]
• Established a Knowledge Distillation framework using PyTorch's FSDP method for distributed computing across multiple nodes and GPUs, utilizing NVIDIA's A10s, H100s, and A100 GPUs. This framework facilitates Knowledge distillation from a teacher model (e.g., Qwen7B or LLaMA7B) to a student model equipped with Quant and DeQuant (QDQ) stubs, supporting both static and dynamic quantization for QAT of the LLM model. [14][15]

References

• [1] LLM.int8(): https://arxiv.org/pdf/2208.07339.pdf
• [2] AWQ (Activation aware Weight Quantization): https://arxiv.org/pdf/2306.00978.pdf
• [3] Smooth Quant: https://arxiv.org/pdf/2211.10438.pdf
• [4] Omni Quant: https://arxiv.org/abs/2308.13137
• [5] GPTQ: https://arxiv.org/pdf/2210.17323.pdf
• [6] GGUF/GGML: https://github.com/ggerganov/ggml
• [7] Flash Attention: https://arxiv.org/abs/2205.14135
• [8] Online normalizer calculation for softmax: https://arxiv.org/pdf/1805.02867
• [9] The Unreasonable Ineffectiveness of the Deeper Layers: https://arxiv.org/abs/2403.17887
• [10] Low-rank pruning of LLaMA2: https://mobiusml.github.io/low-rank-llama2/
• [11] LoRA: https://arxiv.org/abs/2106.09685
• [12] QLoRA: https://arxiv.org/abs/2305.14314
• [13] LoRA+: https://arxiv.org/abs/2402.12354
• [14] LLM-QAT: https://arxiv.org/abs/2305.17888
• [15] PyTorch FSDP: https://arxiv.org/abs/2304.11277

Enhancing CLIP Model Performance through Transformer Block Analysis and Optimization

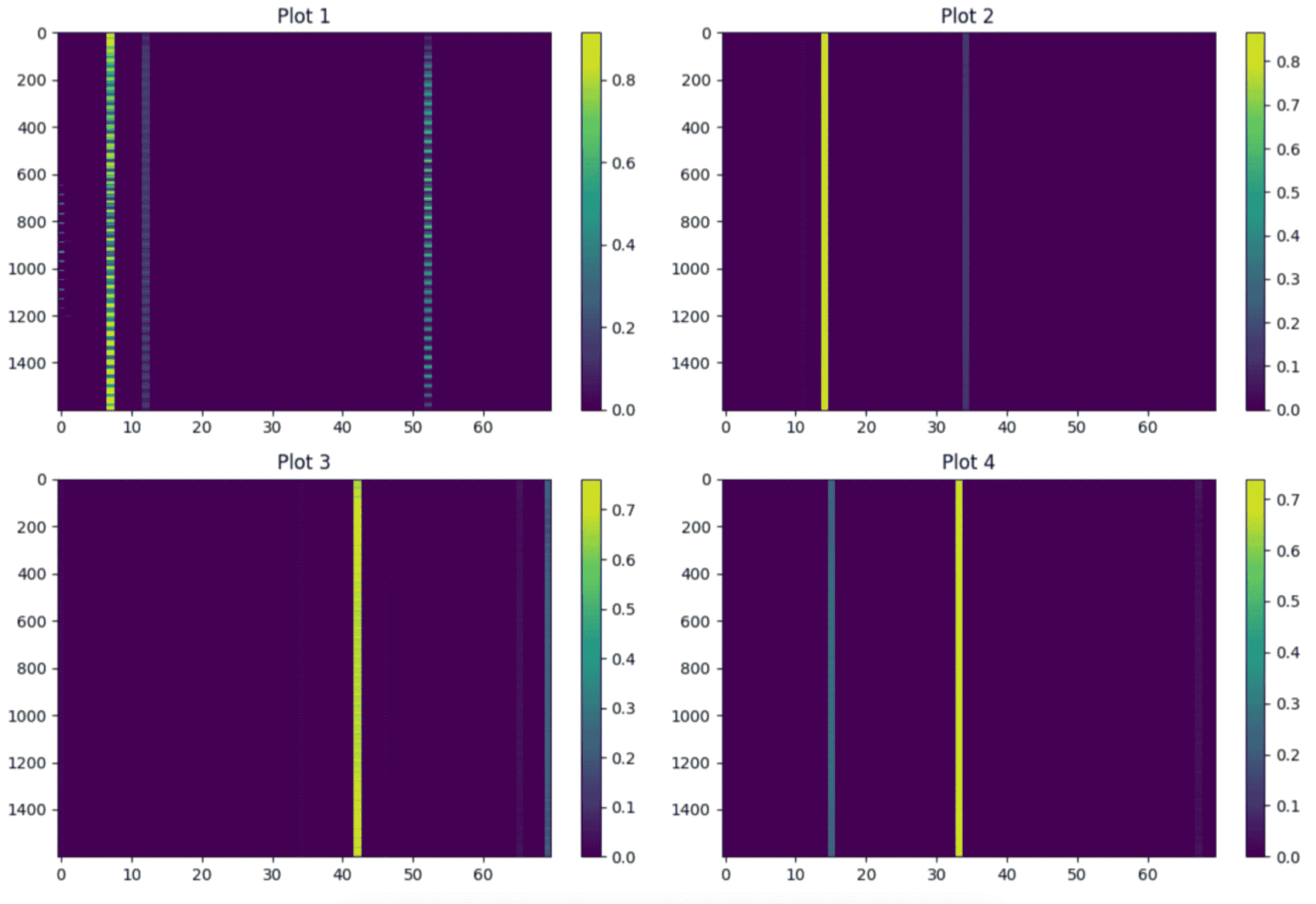
In this study, I concentrated on optimizing OpenAI's CLIP model by enhancing its Transformer blocks, specifically focusing on the Key-Query-Value (KQV) projection layers through quantization observer analysis. The goal is to improve accuracy with minimal performance impact. Additionally, I investigated the impact of quantization errors in mean, variance, and inverse square root in Layer normalization within the Transformer block, proposing corrective measures for performance enhancement. Collaborating with Durga and Titash, we also analyzed systematic outliers in hidden layer features, developing a new quantization computation to mitigate errors arising from these outliers, as illustrated in the figure below.

References

• CLIP Paper
• LLM.int8() Paper

Advancements in Inverse Square Root Approximation for Neural Network Normalization Layers

I (along with Siva) developed an innovative function approximation for efficient ASIC processors, specifically targeting the inverse square root function. Our novel algorithm revolutionizes its application in normalization layers within neural networks, supporting both powers-of-two quantization and scale with zero-point quantization. Compared to existing techniques, our approximation is approximately 2x faster and exhibits a 30% improvement in accuracy. Evaluation metrics, including Mean Squared Error (MSE), Signal-to-Noise Ratio (SNR), and Mean Absolute Error (MAE), showcase significant advancements in both speed and precision.

Results

The diagram below shows the old methods in red and the new method in blue.

The new algorithm's impact on transformer blocks, widely employed in diffusion models, LLMs, and image generation models like Stable Diffusion, is particularly noteworthy. The enhanced precision and computational efficiency contribute significantly to improving inference speeds in Language Models and facilitating the generation of high-quality images in models like Stable Diffusion

Impact of Observers on Rounding Techniques during Quantization Aware Training (QAT)

In this study, I investigated the influence of different observers on the convergence behavior of quantization aware training (QAT) when coupled with various rounding techniques. The observers considered are min_max_observer and moving_average_min_max_observer, and the rounding techniques analyzed include rne_c/c++, rne_python, and rai. The evaluation is conducted across multiple epochs to understand the dynamics of convergence.

Results

References

• Pytorch QAT
• QAT blog

Comparative Analysis of Rounding Techniques in Post Training Quantization for ResNet50 Model

In this study, I systematically explored the impact of different rounding techniques in post-training quantization, specifically focusing on ResNet50 model. The evaluated rounding methods include Rounding Away from Infinity (RAI), Round to Nearest Even (RNE), and Ada-round Simulator.

Results

References:

• AdaRound Paper
• AIMET Presentation
• AIMET Code

Performance Enhancement through Activation Analysis and Precision Optimization in YOLOv5 Models

In this study, I focussed on optimising YOLOv5 accuracy through activation distribution analysis. The quantized model, using Post-Training Quantization (PTQ) without Quantization-Aware Training (QAT), achieved improved precision by selectively offsetting activation functions to claim more bits for higher precision. Subsequent adjustments in the mathematical operations within the network compensated for the changes introduced in the activation layers.

Results

Designed the Math behind Precision-Preserving Kernels for Complex Mathematical Operations such as ROIAlign and Bilinear Interpolation on ASIC

In this study, I introduced efficient kernels design in int8 precision and mathematical optimization for ROIAlign function. Custom ROIAlign kernels ensure accurate region-based feature extraction in computer vision. I addressed the challenges in bilinear interpolation due to quantization errors, emphasizing the importance of preserving precision.

Challenges in Quantizing Bilinear Interpolation:

Small errors in quantization could result in significant shifts in bounding boxes (as shown in the figure above, where the red dot represented the actual FP32 point intended for the pixel within the red box, but quantization errors would shift the point to a new position as represented by the blue dot, resulting in the selection of the pixel represented by the blue rectangle). This shift caused high errors in the bounding boxes, ultimately resulting in incorrect object detections in YOLO models. I successfully navigated this challenge, achieving a quantization strategy that struck a delicate balance between computational efficiency and precision.

Reference

• ROIAlign Paper

Kernel Development for Efficient Powers-of-Two Approximation Exponentiation and Application to SoftMax Function

This research introduced a novel kernel designed for accurate powers-of-two approximation exponentiation. Leveraging polynomial fitting and the Newton-Raphson method, our approach (along with Aditya) optimized the computation of exponentiation, offering a balance between precision and efficiency. The kernel's versatility extends beyond traditional exponentiation applications to include the SoftMax function.

e^x = 2^(x/ln(2))

• Precalculate 1/ln(2)
• Multiply this constant by your argument (1 multiplication)
• Use binary shifts to raise 2 to the integer portion of the power (assumes exp+mantissa format)
• Approximate and quantize the fractional part.
• Adjust based on the fractional power-of-2 remainder (likely a second multiplication)

Reference

• Exponent Approximation

Academic Research

Fine-Tuning and Quantization Techniques for Enhanced Efficiency in LLMs for Task-Specific Code Generation

• Under the mentorship of Satya Uppalapati,
• With guidance from Wajahat Qadeer, Rajashekar Reddy, and Siva Kumar Vemuri.
• Thesis submitted to BITS Pilani, India

Convolutional Neural Networks based Dementia and Tumor Classification from MRI Brain Images

Paper Link Github Code Link

• Under the guidance of Prof. N. Ruban at VIT Vellore.
• Published in IEEE Xplore at CICT Conference

Twitter . LinkedIn . Substack . Medium . GitHub . Instagram . xr4936s4@duck.com